Question

The best leaper in the animal kingdom is the puma, which can jump to a height of 3.7 m when leaving the ground at an angle of 45°. With what speed must the animal leave the ground to reach that height?_____ m/s

Answer 1

Given:

The puma jumps to the height of: h = 3.7 m

The angle made by puma with the ground is: θ = 45°

To find:

The speed of the puma when it leaves the ground.

Step-by-step explanation:

We consider only the vertical motion of the puma.

The puma jumps to the height of 3.7 m and its speed at this height will be zero.

Thus, v = 0 m/s.

The initial speed "u" can be calculated by using the following kinematical equation.

`v^2=u^2+2ah`

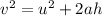
Here, a = - g. The negative sign indicates that the puma jumps against the acceleration due to gravity.

Taking g = 9.8 m/s² and substituting the values in the above equation, we get:

`\begin{gathered} (0\text{ m/s\rparen}^2=u^2+2*(-9.8\text{ m/s}^2)*3.7\text{ m} \\ \\ 0=u^2-72.52\text{ m}^2\text{/s}^2 \\ \\ u^2=72.52\text{ m}^2\text{/s}^2 \\ \\ v=\sqrt{72.52\text{ m}^2\text{/s}^2} \\ \\ u=8.51\text{ m/s} \end{gathered}`

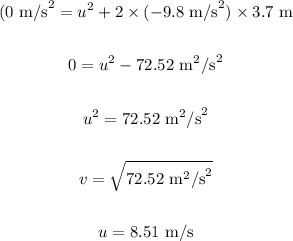
Now, the vertical component of the speed of the puma is given as:

`u=u_0sin\theta`

Here, u0 is the speed with which the puma leaves the ground.

Substituting the values in the above equation, we get:

`\begin{gathered} 8.51\text{ m/s}=u_0sin45\degree \\ \\ u_0=\frac{8.51\text{ m/s}}{sin45\degree} \\ \\ u_0=\frac{8.51\text{ m/s}}{0.707} \\ \\ u_0=12.03\text{ m/s} \\ \\ u_0\approx12\text{ m/s} \end{gathered}`

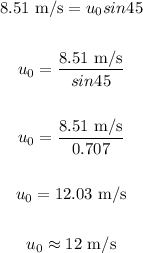
Final answer:

The speed of the puma with which it leaves the ground is 12 m/s.