Finding the height of the base
To find this height, we have that the total volume of this triangular prism can be found as follows:
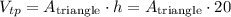
We have that the volume of the prism is equal to 2,400 cubic centimeters. Then, we have:
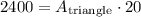
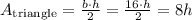
Then, we have:
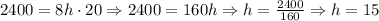
Therefore, the height of this triangular prism is equal to 15cm.
The approximate amount of cardboard used to make the candy box
This is the total surface area of the prism. We can find it, finding the areas of the triangles, and the rectangles in the prism:
Area of the triangle
![A_t=(b\cdot h)/(2)\Rightarrow A_t=(16\cdot15)/(2)\Rightarrow A_t=120\operatorname{cm}^2]()
The area of one of the triangles is 120 sq. centimeters.
Area of one of the rectangles
We have two types of rectangles:
![A_(r1)=20\operatorname{cm}\cdot17\operatorname{cm}=340\operatorname{cm}^2]()
![A_(r2)=20\operatorname{cm}\cdot16\operatorname{cm}=320\operatorname{cm}^2]()
Then, the total area of the triangular prism is:
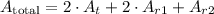
![A_{\text{total}}=2\cdot120\operatorname{cm}+2\cdot340\operatorname{cm}+320\operatorname{cm}\Rightarrow A_(total)=1240\operatorname{cm}^2]()
In summary, we have:
• Height of the base = 15cm
,
• Approximate amount of cardboard = 1240 sq. centimeters.