Question

Find the Cost per game (slope):Find the Shoe Rental Price (y-intercept):

Answer 1

Part A:

To find the slope, we pick the coordinates of any two points from the table.

`\begin{gathered} \text{P icking the points (1,4.50) and (2,7.00)} \\ \\ \text{where;} \\ x_1=1 \\ y_1=4.50 \\ x_2=2 \\ y_2=7.00 \end{gathered}`

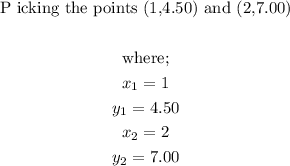
Using the slope formula;

`m=\frac{y_2-y_1}{x_2-x_1_{}}`

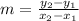
Substituting the points into the formula,

`\begin{gathered} m=\frac{y_2-y_1}{x_2-x_1_{}} \\ m=(7.00-4.50)/(2-1) \\ m=(2.5)/(1) \\ m=\text{ \$2.50} \end{gathered}`

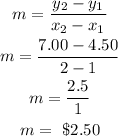
Therefore, the cost per game (slope) is $2.50

Part B:

To get the shoe rental price (y-intercept),

Using the equation of a line in the slope-intercept form,

`\begin{gathered} y=mx+b \\ \text{where b is the y-intercept} \\ m\text{ is the slope} \\ \\ U\sin g\text{ the point (1,4.50) to get the value of b,} \\ x=1 \\ y=4.50 \\ m=2.50 \\ \\ \\ y=mx+b \\ 4.50=2.50(1)+b \\ 4.5-2.5=b \\ b=\text{ \$2.00} \end{gathered}`

Therefore, the shoe rental price (y-intercept) is $2.00