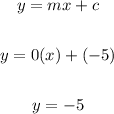Question

Write an equation in slope–intercept form for a line that passes through thepoint (2, –5) and is parallel to y = 11.

Answer 1

Given:

The line passes through points (2, -5)

Parallel to y = 11

Find-:

The equation in slope-intercept form

Explanation-:

The general equation of slope-intercept is:

`y=mx+c`

Compare with the parallel line,

`\begin{gathered} y=mx+c \\ \\ y=11 \\ \end{gathered}`

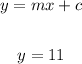
That mean,

`y=(0)x+11`

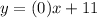
The slope is zero.

The parallel line slope is also the same.

So parallel line equation is:

`\begin{gathered} y=mx+c \\ \\ y=0(x)+c \\ \\ \end{gathered}`

Line pass (2,-5) so,

`\begin{gathered} (x,y)=(2,-5) \\ \\ y=0(x)+c \\ \\ -5=0(2)+c \\ \\ c=-5 \end{gathered}`

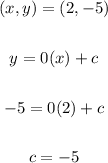
Then equation of line is:

`\begin{gathered} y=mx+c \\ \\ y=0(x)+(-5) \\ \\ y=-5 \end{gathered}`