Question

An Alaskan rescue plane traveling 35 m/s drops a package of emergency rations from a height of 138 m to a stranded party of explorers. gravity is 9.8 where does the package strike the ground relative to the point directly below where it was released? What is the horizontal component of the velocity just before it hits?What is the veriical component of the velocity just before it hits?

Answer 1

Given:

Velocity of plane = 35 m/s

Height = 138 m

g = 9.8 m/s²

Let's solve for the following:

(a) Where does the package strike the ground relative to the point directly below where it was released?

Here, we are to find the horizontal distance.

Apply the formula:

`x=v_ot`

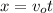
To solve for the time taken to reach the ground, t, apply the formula:

`h=h_0+v_0yt-(1)/(2)gt^2`

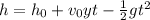
Where:

• h = 0 m

,

• h0 = 138 m

,

• vo = 0

,

• g = 9.8 m/s^2

Thus, we have:

`\begin{gathered} 0=138+0-(1)/(2)*9.8t^2 \\ \\ 0=138+4.9t^2 \\ \\ t=\sqrt[]{(138)/(4.9)} \\ \\ t=5.3s \end{gathered}`

To find the distance, we have:

`\begin{gathered} x=v_0* t \\ \\ x=35\text{ m/s }*5.3 \\ \\ x=185.5\text{ m} \end{gathered}`

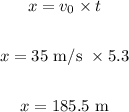
Therefore, the package strikes the ground at 185.5 m relative to the point directly below where it was released.

(b) What is the horizontal component of the velocity just before it hits?

To find the horizontal component of the velocity, we have the formula:

`v_x=v_(0x)=35\text{ m/s}`

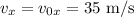
Therefore, the horizontal component of the velocity just before it hits is 35 m/s

(c) What is the veriical component of the velocity just before it hits?

Apply the formula:

`\begin{gathered} v_y=v_(0y)-gt \\ \\ v_y=0-9.8*5.3 \\ \\ v_y=-51.94\text{ m/s} \end{gathered}`

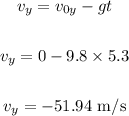
The vertical component of the velocity just before it hits is -51,94 m/s

ANSWER:

• (a) 185.5 m

,

• (b) 35 m/s

,

• (c) -51.94 m/s