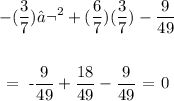Answer:

Step-by-step explanation:
Here, we want to get the maximum/minimum value of the given function
The highest power of the function is 2 and that means it is a quadratic function
Given that the leading coefficient is negative, the function does not have a minimum but a maximum value
To get the maximum value (the y-coordinate of the vertex), we use the following formula:
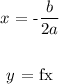
a represents the leading coefficient
b represents the coefficient of x
Substituting the values, we have it that:
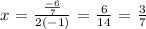
We now substitute this value into the original equation
We have this as follows: