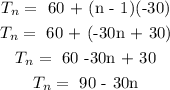Question

(60, 30, 0, -30,...) what is the recursive equation and what is the explicit equation ?

Answer 1

Answer:

Recursive Formula: f(n) = f(n-1) - 30

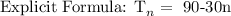
`\text{Explicit Formula: T}_n=\text{ 90-30n}`Explanations:

In a recursive equation, a term is written in terms of the preceding term.

In the sequence 60, 30, 0, -30......

The common difference is (30 - 60) = -30

Which means that a term is written as a function of the preceding term.

If the current term is f(n)

The preceding term is f(n-1)

The number of terms is n

The recursive equation is then:

f(n) = f(n-1) - 30

For the explicit equation:

The sequence 60, 30, 0, -30..... is an Arithmetic Progression (AP)

The formula for the nth Arithmetic Progression is:

`\begin{gathered} T_n=\text{ a + (n-1)d} \\ \text{Where T}_n=\text{ nth term} \\ a\text{ = first term} \\ n\text{ = number of terms} \\ d\text{ = common difference} \end{gathered}`

The common difference, d = 30 - 60 = -30

The first term, a = 60

Substituting these parameters into the formula:

`\begin{gathered} T_n=\text{ 60 + (n - 1)(-30)} \\ T_n=\text{ 60 + (-30n + 30)} \\ T_n=\text{ 60 -30n + 30} \\ T_n=\text{ 90 - 30n} \end{gathered}`