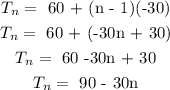Answer:
Recursive Formula: f(n) = f(n-1) - 30
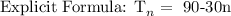
Explanations:
In a recursive equation, a term is written in terms of the preceding term.
In the sequence 60, 30, 0, -30......
The common difference is (30 - 60) = -30
Which means that a term is written as a function of the preceding term.
If the current term is f(n)
The preceding term is f(n-1)
The number of terms is n
The recursive equation is then:
f(n) = f(n-1) - 30
For the explicit equation:
The sequence 60, 30, 0, -30..... is an Arithmetic Progression (AP)
The formula for the nth Arithmetic Progression is:

The common difference, d = 30 - 60 = -30
The first term, a = 60
Substituting these parameters into the formula: