Question

Point P is on segment AB such that AP: PB is 1:3. If A has coordinates (-3,-4)and B has coordinates (5, 0), determine and state the coordinates of P. PLEASE HELP

Answer 1

Here is a sketch of the situation.

Let us now find the distance along x and y coordinates between A and B.

The distance along x coordinate is

`|5--3|\text{ = 8}`

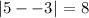
and the distance along y coordinate is

`|0--4|=4`

Now, we know that P is 1/4 the distance from A to B; therefore, we take 1/4 of the x and y coordinates and see where they lead us.

1/4 fo the x coordinate is

`(1)/(4)*8=2`

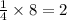
Similarly, 1/4 of the y-coordinate is

`(1)/(4)*4=1`

Now we know that P is found 2 units to the right and 1 unit up from A.

Therefore, P is at

`A(-3+2,-4+1)\rightarrow P(-1,-3)`

Hence, the coordinates of P are (-1, -3)