Question

The prices of 10 single-family, three-bedroomhomes for sale in Santa Rosa, California, arelisted for a recent year. Find the mean, median,and mode (if one exists).$850,000, $835,000, $839,000, $829,000,$850,000, $850,000, $850,000, $847,000,$1,850,000, $825,000

Answer 1

Before we begin solving properly, let us arrange the data given in ascending order:

`\begin{gathered} 825,000; \\ 829,000; \\ 835,000; \\ 839,000; \\ 847,000; \\ 850,000; \\ 850,000; \\ 850,000; \\ 850,000; \\ 1,850,000 \end{gathered}`

MEAN:

The mean is the average of a data set. This can be calculated by finding the sum of the data set and dividing this sum by the number of data considered:

`Mean=\frac{\text{Sum of data}}{Number\text{ of data}}`

For our data set, we have

The mean of the data is $942,500.

MEDIAN:

The median is the middle of the set of numbers. If the number of the set is an even number, we find the mean of the middle two numbers.

In our data set, we have 10 data. Therefore, our median will be the mean of the 5th and 6th data:

`\begin{gathered} 5th\text{ data}\Rightarrow847,000 \\ 6th\text{ data}\Rightarrow850,000 \end{gathered}`

Therefore, the median is given as

`\Rightarrow(847000+850000)/(2)=848,500`

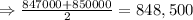
The median of the data is $848,500.

MODE:

The mode of a data set is the particular data that appears the most.

On observation, we can see that $850,000 appears 4 times, more than any other number, and this makes it the median.

The mode of the data is $850,000.