4. The triangle shown is composed of two triangles where b, + b = b. Verify that the area of the entire triangle is equivalent to the sum of the areas of Triangles A and B.

Question

asked Apr 27, 2023 73.7k views

1 Answer

Chethaka Uduwarage · Answer 1 · 2023-05-03T19:23:06+0000

Given : the triangle shown is composed of two triangles where

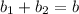
The height of both triangles is the same as the height of largest triangle

The area of the triangle A =

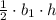
$(1)/(2)\cdot b_1\cdot h$

The area of the triangle B =

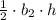
$(1)/(2)\cdot b_2\cdot h$

The sum of the area of the triangles A and B =

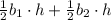
$(1)/(2)b_1\cdot h+(1)/(2)b_2\cdot h_{}$

Take 1/2 h as a common:

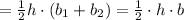
$=(1)/(2)h\cdot(b_1+b_2)=(1)/(2)\cdot h\cdot b$

So, the area of the entire triangle is equivalent to the sum of the areas of Triangles A and B.