Question

I need help with making graphs and identifying the slope and gradient of it.

Answer 1

Given:

Find-: Graph and rate of change.

Sol:

Rate of change :

The rate of change is used to mathematically describe the percentage change in value over a defined period of time, and it represents the momentum of a variable.

`\text{ Slope = }(y_2-y_1)/(x_2-x_1)`

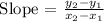
Where,

`\begin{gathered} (x_1,y_1)=(1,1.25) \\ \\ (x_2,y_2)=(2,2.4) \end{gathered}`

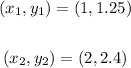
So the slope is:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \\ m=(2.4-1.25)/(2-1) \\ \\ m=1.15 \end{gathered}`

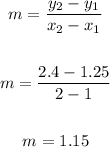
The general form of the equation is:

`\begin{gathered} y=mx+c \\ \\ y=1.15x+c \end{gathered}`

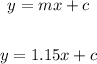
The value of "c" is:

`\begin{gathered} (x,y)=(1,1.25) \\ \\ y=1.15x+c \\ \\ 1.25=1.15(1)+c \\ \\ c=1.25-1.15 \\ \\ c=0.10 \end{gathered}`

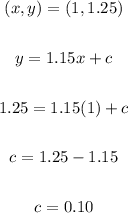
So equation of a line is:

`\begin{gathered} y=mx+c \\ y=1.15x+0.10 \end{gathered}`

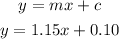
The graph of the line is: