We have a parabola.
We know that, at the center, x=0, the height is 54.
So we have the vertex of the parabola at (0,54).
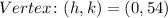
As the clearance at height y=8 is 18, we know that for points x=-18/2=-9 and x=18/2=9, the value of y is y=8.
We have two points of the parabola:
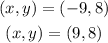
We can use the vertex form to describe the parabola:
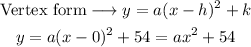
We use one of the points to find the value of the parameter a:
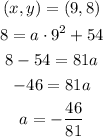
Then, the equation becomes:
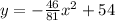
Answer: y=-46/81*x^2+54
We can graph this as: