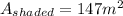Answer: We need to find the area of the shaded region in the given figure:
This shaded region can be broken into three parts as follows:
We can find the area of each of these (1) (2) and (3) boxes and sum it all together to get the total area.
(1)
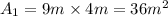
(2)
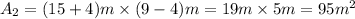
(3)
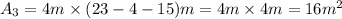
Adding them together gives.
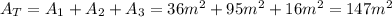
Therefore: