Step-by-step explanation
Since each member of the committee has a distinct responsibility, this means that the order of selection matters. A different order means that two people would have different responsibilities. So we conclude that we must compute the possible arrangements using permutation.
We have:
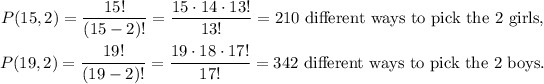
Multiplying these results, we get the total number of ways to form the committee:
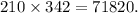
Answer
To compute the number of possible arrangements we use permutation, and there are 71820 ways to form the committee.