Question

What are all the possible rational roots of 2x^3-x^2-2x+1

Answer 1

The given expression can be rewritten as;

`x^2(2x+1)\text{ -}(2x+1)`

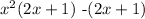
If we expand the above equation, we'll still have the same expression in the question.

We can now factorize, which will give us;

`(x^2-1)(2x+1)`

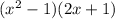
We apply the difference of two squares , we'll then have;

`x^2-1\text{ = }(x^2-1^2)=\text{ }(x-1)(x+1)`

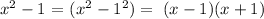
So, we'll then have the below as factors;

`(x-1)(x+1)(2x+1)`

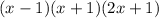
The roots of the polynomial then will be 1, -1, -1/2 which we'll get from equating each factor to zero and solving for x.