Question

A painter needs to cover a triangular region 60 meters by 77 meters by 89 meters…..

Answer 1

We first try and construct the triangular region

We will first find the area of th above triangle

Since we are given just the three sides, we will therefore use the Hero's Formula

Using the above formula, we will have

`\begin{gathered} S=(60+77+89)/(2) \\ S=(226)/(2) \\ S=113 \end{gathered}`

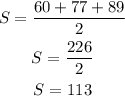
The Area of the triangle will be

`\begin{gathered} A=\sqrt[]{S(S-a)(S-b)(S-c)} \\ A=\sqrt[]{113(113-60)(113-77)(113-89)} \\ A=\sqrt[]{113(53)(36)(24)} \\ A=\sqrt[]{5174496} \\ A=2274.751855m^2 \end{gathered}`

Now, We are given that

A can of Paint covers 80 squares meter area.

and we are also given that the painter can only purchase full can

Therefore, The number of cans of paint (n) needed will be

`\begin{gathered} n=(2274.751855)/(80) \\ n=28.43439819 \end{gathered}`

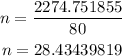
From the above calculation, The Painter needs more than 28 paints

Thus, The Painter will need 29 cans of paint

29 Cans of Paint