Answer:
The scale factor used for the snew building = 9/10
Explanations:
Let the volume of the old building be V₁
Let the volume of the new building be V₂
The volume of the old bulding, V₁ = 21000 ft cube
The volume of the new building = The volume of the old building
V₁ = V₂ = 21000
The volume of a rectangular pyramid is given as:
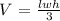
Where l is the length of the base
w is the width
h is the height of the pyramid
The length of the base is scaled by 2/3

The width is scaled by 5/3

The volume of the initial building is:
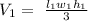
The volume of the new building will be:
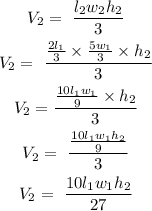
Divide V₂ by V₁
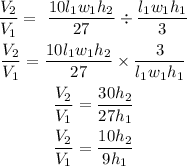
Since V₂ = V₁, V₂ / V₁ = 1
The equation above then becomes:
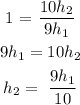
The new building will be scaled by a factor of 9/10 to make the volume of the new building the same as the existing building.