Question

11TimAtt8хGiven: W XY is a line and ZWXZ = 135Prove: 45 = m2ZXYComplete the proof. Number your reasons in the textbox below.ReasonsStatementsWXY is a line and ZWXZ = 135mZW XY = 180°1.2.mZW XY = m2WXZ + m2ZXY3.4.180 = 135 + m2ZXY45 = m2ZXY5.EditView Insert FormatTools Table

Answer 1

Statements and reasons.

1) WXY is a line and ∠WXZ = 135°

Reasons: This statement is true because it is stated in the question.

2) m∠WXY = 180°

Reasons: This statement is true because the angle of a straight line is always 180°.

3) m∠WXY = m∠WXZ + m∠ZXY

Reasons: This statement is true because the angles on one side of a straight line (m∠WXZ and m∠ZXY) always add to 180°.

4) 180° = 135° + m∠ZXY

Reasons:

- by the definition of the question, we know that ∠WXZ = 135° (statement 1)

- from statement 2 we know that m∠WXY = 180° (statement 2)

- replacing the angles of statement 1 and 2 in the equation of statement 3 we find the equation: 180° = 135° + m∠ZXY

5) 45° = m∠ZXY

Reasons: From statement 4 we find that:

`\begin{gathered} 180^(\circ)=135^(\circ)+m\angle ZXY \\ m\angle ZXY=180^(\circ)-135^(\circ) \\ m\angle ZXY=45^(\circ) \end{gathered}`

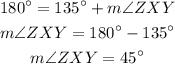
In summary, the reasons are:

1) It is stated in the question.

2) The angle of a straight line is always 180°.

3) The angles on one side of a straight line add 180°.

4) Replacing statement 1 and 2 in statement 3.

5) Solving for m∠ZXY the equation of statement 4.