Question

QuestionFind the equation of a line that contains the points (-5,2) and (4,6). Write the equation in slope-intercept form, usingfractions when required.

Answer 1

First, we have to find the slope using the following formula.

`m=(y_2-y_1)/(x_2-x_1)`

Where,

`\begin{gathered} x_1=-5 \\ x_2=4 \\ y_1=2 \\ y_2=6 \end{gathered}`

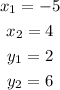
Let's use the coordinates above to find the slope.

`m=(6-2)/(4-(-5))=(4)/(4+5)=(4)/(9)`

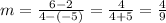
Now, let's use the point-slope formula to find the equation of the line.

`y-y_1=m(x-x_1)`

Where,

`\begin{gathered} m=(4)/(9) \\ x_1=-5 \\ y_1=2 \end{gathered}`
`\begin{gathered} y-2=(4)/(9)(x-(-5)) \\ y-2=(4)/(9)(x+5) \\ y-2=(4)/(9)x+(20)/(9) \\ y=(4)/(9)x+(20)/(9)+2 \\ y=(4)/(9)x+(38)/(9) \end{gathered}`

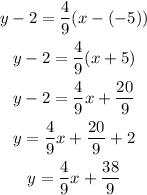
Therefore, the equation in slope-intercept form is y = 4/9x + 38/9.