We need to divide the next rational expressions:
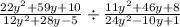
The first thing that we need to do is factorize the denominators and numerators, maybe we can cancel some terms.
The expression cant be factorized, now we are going to divide the terms:
Change the second fraction, now the denominator is the numerator:
Then change the division sign to the multiplication sing *
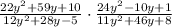
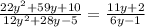
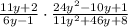
Multiply the expression and reduce the fraction if it is possible:
Factorize the expression:
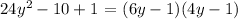
Now, we have the expression like this:
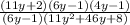
Cancel the similar terms 6y-1:

Factorize 11y^2 + 46y + 48
=(11y^2+2y) + (44y+8)
Factorize y from (11y^2+2y)
=y(11y+2)
Factorize 4 from 44y+8
= 4(11y+2)
So the solution is:
=(11y+2)(y+4)
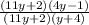
Cancel common terms 11y+2
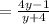
Where 4y-1 is my numerator and y+4 my denominator.