Question

3. Graph the system of linear inequalities. Show work for writing inequalitiesin slope-intercept form. Make sure the solution region is clear in your graph.2x <-y +9-2y -6 ≥ -2x

Answer 1

The first step is to rearrange the inequalities. The first inequality would be

The second inequality would be

`y\text{ }<\text{ 2x - 9}`

`-\text{ 2y }\ge\text{ - 2x + 6}`

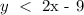
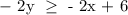
We would divide both sides by - 2. This would cause the inequality symbol to reverse. It becomes

`y\text{ }\leq\text{ x - 3}`

The next step is to plot both inequalites like normal linear equations

For the first inequality,

y = 9 - 2x

Let us input values for x to get corresponding y values

when x = -2, y = 13

When x = - 1, y = 12

When x = 0, y = 9

When x = 1, y = 7

When x = 2, y = 5

For the second inequality,

y = x - 3

Let us input values for x to get corresponding y values

when x = -2, y = - 5

When x = - 1, y = - 4

When x = 0, y = - 3

When x = 1, y = - 2

When x = 2, y = - 1

We would plot these points on a graph and we would get 2 straight lines.

The graph is shown in the attached photo.

The solution region is the darker region