Use the function f and the given real number a to find (f -1)'(a). (Hint: See Example 5. If an answer does not exist, enter DNE.)f(x) = cos(2x), 0 ≤ x ≤ /2, a = 1

Question

asked Mar 10, 2023 229k views

1 Answer

Benjumanji · Answer 1 · 2023-03-14T02:44:54+0000

The answer is:

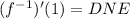
$(f^(-1))^(\prime)(1)=DNE$

Step-by-step explanation:

We need to use the theorem for the inverse of the derivative:

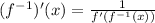
$(f^(-1))^(\prime)(x)=(1)/(f^(\prime)(f^(-1)(x)))$

Then, we need to calculate the derivative of f and its inverse.

To find the derivative, we know that the derivative of cosine is negative sine, and by the chain rule:

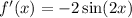
$f^(\prime)(x)=-2\sin(2x)$

ANd to find the inverse, we call f(x) = y and solve for x:

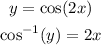
$\begin{gathered} y=\cos(2x) \\ \cos^(-1)(y)=2x \\ \end{gathered}$
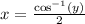
$x=(\cos^(-1)(y))/(2)$

Now, we switch the variables, and we have the inverse:

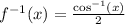
$f^(-1)(x)=(\cos^(-1)(x))/(2)$

And now, by the theorem:

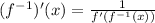
$(f^(-1))^(\prime)(x)=(1)/(f^(\prime)(f^(-1)(x)))$

To find the derivative of the inverse in x = 1, we need to find first:

$f^(-1)(1)=(\cos^(-1)(1))/(2)=(0)/(2)=0$

Now:

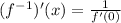
$(f^(-1))^(\prime)(x)=(1)/(f^(\prime)(0))$
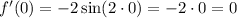
$f^(\prime)(0)=-2\sin(2\cdot0)=-2\cdot0=0$

And finally:

$(f^(-1))^(\prime)(x)=(1)/(0)=DNE$

Thus, the correct answer is DNE