Question

Determine the depth of water if an echo using sonar returns in 870 ms and the speed of sound in water is 5300 km/h.

Answer 1

253.8 m

Step-by-step explanation

Given:

• time of the return of the echo, t = 870 ms

,

• the speed of sound in water, s = 5300 km/h

We have to find the depth of water, x.

The sonar emits a signal that travels through the water to the bottom and then the echo travels back, so the time it takes the echo to return to the sonar is the time it takes the signal to travel the depth of the water twice - to the bottom and back,

The speed is,

`s=(x)/(t)`

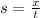
We know that x is 2h,

`s=(2h)/(t)`

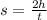
Solving for h,

`h=(s\cdot t)/(2)`

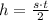
Now we have to put the values of the speed and the time, but their units are different. We have to transform the time from milliseconds to hours.

1 hour has 3,600 seconds, which is 3,600,000 milliseconds,

`870ms\cdot(1h)/(3,600,000ms)=0.00024h`

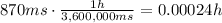
Now we can replace into the equation to find h,

The depth of water is 253.8m.