To solve the exercise we can first find the slope that passes through the given points using this formula

So, in this case, we have

As this line has a slope of zero, then it is a horizontal line, which implies that y is constant, that is, and always takes the same value. Its equation is

Therefore, the equation of the line through the line given points is
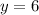
As you can see in the graph