Question

Jarod is having a problem with rabbits getting into his vegetable garden, so he decides to fence it in. The length of the garden is 5 feet more than 2 times the width. He needs 58 feet of fencing to do the job. Find the length and width of the garden.

Answer 1

Let's call the length of the fence as L and the width of the fence as W. From the first statement, we get a relation between those two.

"The length of the garden is 5 feet more than 2 times the width."

From this sentence, we know that

`L=5+2W`

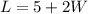
And from the statement

"He needs 58 feet of fencing to do the job."

We know that the perimeter should add up to 58 feet. The perimeter is the sum of the sides, then, it is two times the width plus two times the length.

`2L+2W=58`

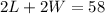
Now, we have a system with two equations and two variables.

`\begin{cases}2L+2W=58 \\ L=5+2W\end{cases}`

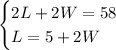
We can divide the first one by two on both sides of the equality

`\begin{cases}L+W=29 \\ L=5+2W\end{cases}`

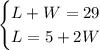
If we substitute our L in the second equation for the L in the first equation, we get an equation only for W.

`\begin{gathered} (5+2W)+W=29 \\ 5+3W=29 \\ W=(29-5)/(3)=8 \end{gathered}`

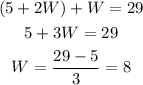
Now that we know the width, we can calculate the length.

`L=5+2W\Rightarrow L=5+2*8=5+16=21`

The length of the fence is 21 feet, and the width is 8 feet.