Question

Write a polynomial in standard form that meets the following conditions. Assume a=1 and your function is f(x), The zeros are -1/2, 2, and -6.

Answer 1

f(x) = x³ + (9/2)x² - 10x - 6

Step-by-step explanation:

A polynomial with zeros at b, c, d has the following form

f(x) = a(x - b)(x - c)(x - d)

Where a is the leading coefficient.

In this case, a = 1, and the zeros are -1/2, 2, and -6. Then, we can write the polynomial as follows

`\begin{gathered} f(x)=1(x-(-1/2))(x-2)(x-(-6_{})) \\ f(x)=(x+(1)/(2))(x-2)(x+6_{}) \end{gathered}`

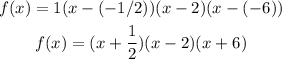
To write it in standard form, we need to expand the expression, so

`\begin{gathered} f(x)=(x(x)+x(-2)+(1)/(2)(x)+(1)/(2)(-2))(x+6) \\ f(x)=(x^2-2x+(1)/(2)x-1)(x+6) \\ f(x)=(x^2-(3)/(2)x-1)(x+6) \\ f(x)=x^2(x)+x^2(6)-(3)/(2)x(x)-(3)/(2)x(6)-1(x)-1(6) \\ f(x)=x^3+6x^2-(3)/(2)x^2-9x-x-6 \\ f(x)=x^3+(9)/(2)x^2-10x-6 \end{gathered}`

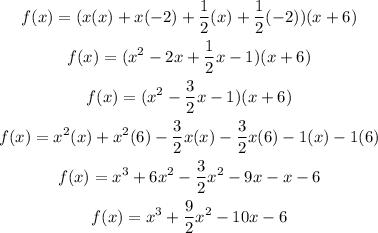
Therefore, the polynomial in standard form is

f(x) = x³ + (9/2)x² - 10x - 6