Question

3. From 2005 to 2015, a population of lions is modeled by the equation = 1500 · (0. 98)^t where t is the number of years since 2005.a. About how many lions were there in 2005?b. Describe what is happening to the population of lions over this decade.c. About how many lions are there in 2015? Show your reasoning

Answer 1

ANSWER and EXPLANATION

The population of lions is modeled by the equation:

`P=1500\cdot(0.98)^t`

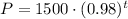
where t = number of years since 2005.

(a) To find the number of lions there in 2005, we have to find P when t is 0:

`\begin{gathered} P=1500\cdot(0.98)^0 \\ P=1500\cdot1 \\ P=1500\text{ lions} \end{gathered}`

There were 1500 lions.

(b) The given function is an exponential function. The exponential factor in the function is 0.98.

In an exponential function, when the exponential factor is less than 1, it means that the function is a decay, hence, it is a decreasing function.

Hence, the population of lions was decreasing over the decade.

(c) Since 2015 is 10 years after 2005, to find the population of lions in 2015, we have to find P when t is equal to 10.

That is:

`\begin{gathered} P=1500\cdot0.98^(10) \\ P=1500\cdot0.8171 \\ P\approxeq1,226\text{ lions} \end{gathered}`

That is the answer.