The sequence can be found using an arithmetic sequence:

Where:
a1 = First term
d = Common difference
so:
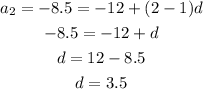
Therefore, the sequence is given by:
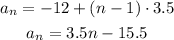
Let's find the limit of the function associated to an:
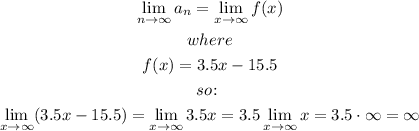
Therefore, since the limit of the function associated to the sequence tends to infinity, we can conclude that the sequence diverges