Question

Find the area of the missing square off to leg b if the area of one square is 369 and the area of another is 81

Answer 1

We have three squares, which sides are the same of a square triangle.

We know the area of 2 out of the 3 squares. We have to find the area of the third.

The area of the smaller square is 81. As b it is side, the area of the square is b^2=81.

The area of the biggest triangle is c^2=369.

The area we need to find has a value of a^2.

As we have a square triangle, we can apply the Pythagorean theorem:

`a^2+b^2=c^2^{}`

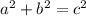
As we already know the values of b^2 and c^2, we can find the area of the square as:

`\text{Area}=a^2=c^2-b^2=369-81=288`

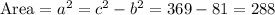
Answer: the area of the square is a^2=288.