Since the numbers 7, 24, 25 form a Pythagorean triple
Then the similar triangle to this triangle must have multiple sides of 7, 24, 50 and make also Pythagorean triple
Let us check the answers
14, 48, 50
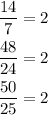
All sides have an equal ratio
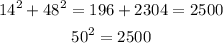
They are a Pythagorean triple
Then 14, 48, 50 is similar to the given triangle
The first answer is correct
The 6th answer is 35, 120, 125
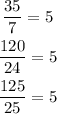
All sides have the same ratio
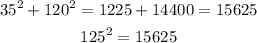
Then 35, 120, 125 make Pythagorean triple
The 6th answer is correct
The answers are:
14, 48, 50 ------- 1st answer
35, 120, 125 ------ 6th answer