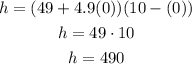The function that models the hight of an object after some time t is:
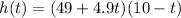
a) when the object hits the ground the hiht will be equal to 0 so we replace and slve for t:
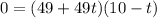
and solving for t will be:
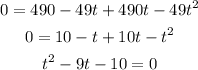
and we solve it with the cuadratic function so:
![\begin{gathered} t=\frac{9\pm\sqrt[]{9^2-4(1)(-10)}}{2(1)} \\ t=\frac{9\pm\sqrt[]{81+40}}{2} \\ t=\frac{9\pm\sqrt[]{121}}{2} \\ t_1=(9+11)/(2) \\ t_1=(20)/(2) \\ t_1=10 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/t2s03xgjrqglu3pht0ugvuwnrq8dnjokge.png)
it takes 10 second to reach the ground.
b) to find the hight the object was drop we can replace t=0 that is the exact tiem whre the object was dropt so: