Question

Find all angles 0 (theta) such that zero degree is less than or equal to theta and less than or equal to 360 degrees for which the statement sin (-104 degrees) = sin 0 theta is true

Answer 1

Step-by-step explanation

So basically we must find an angle between 0° and 360° that meets the following:

`\sin(-104^(\circ))=\sin\theta`

First of all it's important to recall a property of the sine:

`\sin x=\sin(x+360^(\circ))`

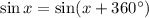
Then if we take x=-104° we get:

`\sin(-104^(\circ))=\sin(-104^(\circ)+360^(\circ))=\sin256^(\circ)`

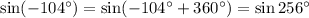
So for now we know that 256° is one value of theta.

For all the angles between 0° and 360° there are always two angles that share the same sine. For any angle in the first quadrant (0° to 90°) there's another angle in the second quadrant (90° to 180°) that has the same sine. The same happens with the third (180° to 270°) and fourth quadrant (270° to 360°). 256° is in the third quadrant which means that there's another possible theta in the fourth quadrant. The difference between this angle and 270° must have the same absolute that the difference between 256° and 270°. Then for the new theta we have:

`\begin{gathered} \lvert{270^(\circ)}-256^(\circ)\rvert=\lvert{\theta-270^(\circ)}\rvert \\ 14^(\circ)=\lvert{\theta-270^(\circ)}\rvert \end{gathered}`

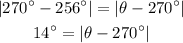
Since theta is part of the fourth quadrant is greater than 270° so the term inside the absolute value is positive and we can get rid of the module:

Then we add 270° to both sides:

Answer

Then the answers are 256° and 284°.