Given that the grant writer wants to increase all the amounts by 4% for Year 2, by 2.5% for Year 3, and by another 2% for Year 4, you can convert each percent to a decimal number by dividing them by 100:
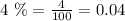
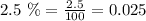
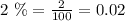
• You know that in Year 1, the amount of money budgeted for Salaries and benefits is $115,000. Therefore:
- In Year 2 it will be (in dollars):
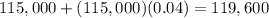
- In Year 3:
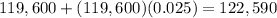
- In Year 4:
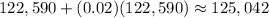
• Apply the same procedure for Insurances, knowing that, for Year 1 the budget is $14,500:
- In Year 2:
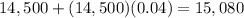
- In Year 3:
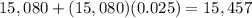
- In Year 4:
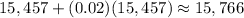
• For Resources and Supplies, you get:
- In Year 2:
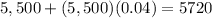
- In Year 3:
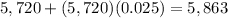
- In Year 4:
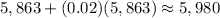
Hence, the answer is: