Question

Do you prefer to express solutions to inequalities using interval notation or as an inequality? Do you think it is important to know both formats? How could each be used?Your response should be 3-5 sentences long and show that you’ve thought about the topic/question at hand, there is not a single “correct answer.”

Answer 1

We have the question for which we have to say our preferences about using interval notation or inequality to express a solution to an inequality.

And we have to determine:

• If it is important to know about both formats

,

• And how could each of them be used

Preference

Then we can say that I prefer to express solutions to inequalities using interval notation since we can easily determine which numbers are in the solution, and also which of them is included or not in the solution by simply adding a square bracket ([ or ]) or a parenthesis ( ( or ) ). For instance, if a have the next solution:

`[5,11)`

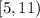
We can easily see that the solutions are between 5 (included) and 11 (not included).

Do you think it is important to know both formats?

Yes, it is important to know about both formats, and they are very common as universal ways to express the solutions to inequalities. In some cases, we encounter books that express the solutions in one way or another. Then we need to be aware of both formats.

How could each be used?

Interval notation: it is very valuable when we have solutions between two different values such as the one explained above [5, 11). However, it is highly precise to express any solution for an inequality, since we can also express solutions of the form:

`\lbrack0,\infty),(-\infty,\infty),(-1,1),...`

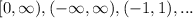
Expressing a solution as an inequality: we can use this notation (or format) when it is sufficient to know one of the values of the solution since the solution would correspond to an open interval of the form:

`x\ge-1`

In this case, the solution is for all numbers greater (and equal) to -1 to the positive infinity. The equivalent for this, in interval notation, is:

`\lbrack-1,\infty)`

If we needed to express the solution expressed in interval notation as [5,11), as an inequality, we have to write it as follows:

`x\ge5,x<11`

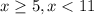
And we have to use two expressions.

In summary, therefore, we can conclude that:

• I prefer to express solutions to inequalities using interval notation since we can easily determine which numbers are in the solution, and also which of them is included or not in the solution by simply adding a square bracket, [, or, ], or a parenthesis, (, or, ).

• Both formats are important since they are very common as universal ways to express the solutions to inequalities. We can see both notations (or formats) used in every mathematics book, and the solutions are expressed in one way or another. Then we need to be aware of both formats.

• The interval notation is very valuable when we have solutions between two different values that are relatively near to each other such as [-5, 0). However,, ,it is highly precise to express any solution(s) for an inequality,. We can use inequality notation when it is sufficient to know one of the values of the solution since the solution would correspond to an open interval, most often when the solution goes to positive or negative infinity.