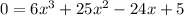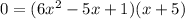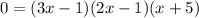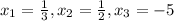Answer:
See below for answers
Explanation:
1) The Fundamental Theorem of Algebra states that in an nth-degree polynomial, there are n zeroes at most, including those that are complex. Therefore, there are 6 zeroes in the function since it's a 6th-degree polynomial.
2) Reduce the polynomial and use the Zero Product Property: