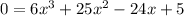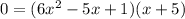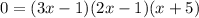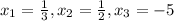Question

1. According to the fundamental theorem of algebra, how many zeros does the function
`f(x) = 3x^6 - 7x^5 - 53x^3 - 43x - 34` have?

2. What are the zeros of
`f(x) = 6x^3 + 25x^2 - 24x + 5`

Answer 1

See below for answers

Explanation:

1) The Fundamental Theorem of Algebra states that in an nth-degree polynomial, there are n zeroes at most, including those that are complex. Therefore, there are 6 zeroes in the function since it's a 6th-degree polynomial.

2) Reduce the polynomial and use the Zero Product Property:

`0=6x^3+25x^2-24x+5`

`0=(6x^2-5x+1)(x+5)`

`0=(3x-1)(2x-1)(x+5)`

`x_1=(1)/(3),x_2=(1)/(2),x_3=-5`