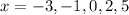Answer:
From the given graph y=f(x),
To find,
a)f'(-4),
Step-by-step explanation:
we know that, Slope at the point -4 is f'(-4),
From the graph,
From the definition of differentiation we get, using the slope formula we get,
(-5,0) and (-4,1), we get,
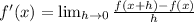
Slope at the point -4 is f'(-4),
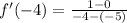
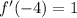
b) To find f'(4)
we know that, Slope at the point 4 is f'(4),
From the definition of differentiation we get, using the slope formula we get,
(3,0) and (5,1), we get, (since the required points lies between (3,0) and (5,1))
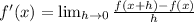
Slope at the point 4 is f'(4),
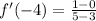

c) Determine all x values where f'(x) is undefined.
The slope of the vertical line is undefined.
Here, for the given graph f(x), there is no vertical line.
Hence the f(x) is defined for all values of x.
There is no x values that f(x) is undefined.
d) Determine all x values where f'(x)=0
To find the x value where slope of f(x) is zero.
It is the point that defines the maximum and minimum of f(x),
From the graph we get that,