Question

Exercises 12.3 Complete the following Complete the senares for each quadratic, is the center and takes the sachach Labeling its translated center (a) x^2+2x+y^2-4y=4(c) 2x^2+2y^2+3x-5y=2

Answer 1

a) We have to find the equation of the quadratic expression.

We have the expression:

`x^2+2x+y^2-4y=4`

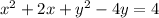
We can grouop the terms for y and x and find the constants we need to form a perfect binomial (completing the squares):

`\begin{gathered} (x^2+2x+1-1)+(y^2-4y+4-4)=4 \\ \lbrack(x+1)^2-1\rbrack+\lbrack(y-2)^2-4\rbrack=4 \\ (x+1)^2+(y-2)^2-1-4=4 \\ (x+1)^2+(y-2)^2=4+1+4 \\ (x+1)^2+(y-2)^2=9 \\ (x+1)^2+(y-2)^2=3^2 \end{gathered}`

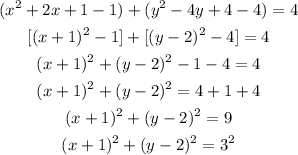
The expression results in a circumference of radius 3 with the center ar (-1,2).

c) If we have the equation:

`2x^2+2y^2+3x-5y=2`

We can solve this as:

`\begin{gathered} 2(x^2+y^2+(3)/(2)x-(5)/(2)y)=2 \\ \lbrack x^2+(3)/(2)x+((3)/(4))^2-((3)/(4))^2\rbrack+\lbrack y^2-(5)/(2)y+((5)/(4))^2-((5)/(4))^2\rbrack=1 \\ \lbrack(x+(3)/(4))^2-(9)/(16)\rbrack+\lbrack(y-(5)/(4))^2-(25)/(16)=1 \\ (x+(3)/(4))^2+(y-(5)/(4))^2=1+(9)/(16)+(25)/(16) \\ (x+(3)/(4))^2+(y-(5)/(4))^2=(16+9+25)/(16) \\ (x+(3)/(4))^2+(y-(5)/(4))^2=(50)/(16) \end{gathered}`

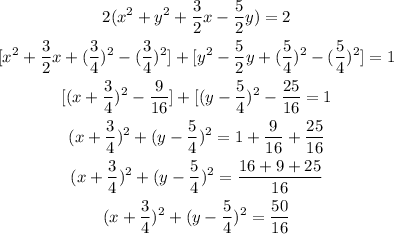
We can calculate the radius as:

`r=\sqrt[]{(50)/(16)}=\sqrt[]{(2\cdot25)/(16)}=\sqrt[]{2}\cdot(5)/(4)=(5)/(4)\sqrt[]{2}`