Question

Use the standard normal table to find the Z-score that corresponds to the cumulative area 0 2546. If the area is not in the table, use the entry closest bto the area. If thearea is halfway between two entries, use the z-score halfway between the corresponding Z-scores Z=_(Type an integer or decimal rounded to two decimal places as needed)

Answer 1

We have to find the z-score that correspond to an area under the curve of 0.2546.

This means to find the value of zc, so that:

Then, we can express zc as:

[tex]z_c=-(0.6+0.06)=-0.66" src="

We can check with an app as:

We have confirmed we have the right value:

`P(z<-0.660)\approx0.2546`

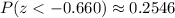
Answer: z-score = -0.66