Question

This table shows the relationship between the amount of time a zebra runs at maximum speed and the distance it travels. a) Write an equation to describe this relationship __________________________b) Apply the equation to find the distance the zebra would travel in 48 minutes __________________________________

Answer 1

We can use the first tio ordered pairs (3,2) and (6,4) to find the rate of change:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ (x_1,y_1)=(3,2) \\ (x_2,y_2)=(6,4) \\ \Rightarrow m=(4-2)/(6-3)=(2)/(3) \\ m=(2)/(3) \end{gathered}`

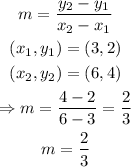
then, using the first ordered pair, we can find the relation function:

`\begin{gathered} y-y_1=m(x-x_1) \\ \Rightarrow y-2=(2)/(3)(x-3)=(2)/(3)x-2 \\ \Rightarrow y=(2)/(3)x-2+2=(2)/(3)x \\ y=(2)/(3)x \end{gathered}`

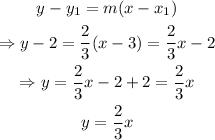
thus, the equation that describes the relationship is y = 2/3 x

Next, to find the distance of the zebra after 48 minutes, we have to make x = 48 and solve for y:

`\begin{gathered} x=48 \\ \Rightarrow y=(2)/(3)\cdot(48)=(96)/(3)=32 \\ y=32 \end{gathered}`

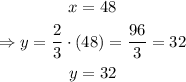
therefore, the zebra would travel 32 miles in 48 minutes