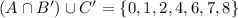1 Answer

TERMIN · Answer 1 · 2023-12-31T06:00:55+0000

We have

U={0,1,2,3,4,5,6,7,8}

A={0,2,4,6,8}

B={1,3,5,7}

C={3,4,5,6}

Then let's calculate the complements

A'={1,3,5,7}

B'={0,2,4,6,8}

C'={0,1,2,7,8}

∪ means union that means that we need to put together both sets in the new set

∩ means intersection that means the new set will be composed only by the elements that share both sets that are intersecting

a.

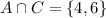
$A\cap C=\mleft\lbrace4,6\mright\rbrace$

b.

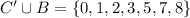
$C^(\prime)\cup B=\mleft\lbrace0,1,2,3,5,7,8\mright\rbrace$

c.

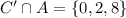
$C^(\prime)\cap A=\mleft\lbrace0,2,8\mright\rbrace$

d.

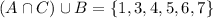
$(A\cap C)\cup B=\mleft\lbrace1,3,4,5,6,7\mright\rbrace$

e.

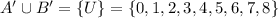
$A^(\prime)\cup B^(\prime)=\mleft\lbrace U\mright\rbrace=\mleft\lbrace0,1,2,3,4,5,6,7,8\mright\rbrace$

f.

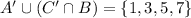
$A^(\prime)\cup(C^(\prime)\cap B)=\mleft\lbrace1,3,5,7\mright\rbrace$

g.

$(A\cap B^(\prime))\cup C^(\prime)=\mleft\lbrace0,1,2,4,6,7,8\mright\rbrace$

Please log in or register to add a comment.