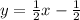Given the equation y=-2x+4, we can easily find the slope of the perpendicular line by calculating the inverse negative of the slope. This is:
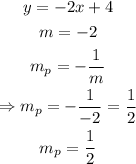
Now that we have the slope, we can ouse the equation slope-intercept to find the intercept b using the point (-3,-2):
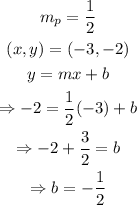
Therefore, the equation in slope-intercept form is: