Let's take the length as x and the width as y.
According to the statement, the width is 6 less than the length, it means the width is x-6. It is also said that the area is 135, it means that the width times the length is 135.
Use this information to find the length and the width.

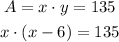
Write the quadratic equation:

Solve for x (use the quadratic formula):
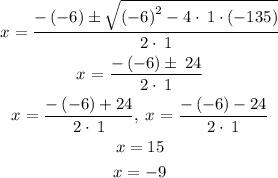
In this case, we have to use only positive values of x, because the length of a rectangle can not be negative. It means, the length of the rectangle is 15 and the width (which is 6 inches less) is 9.
Length=15 inches
Width=9 inches