we can write two equations for the statement, and the solve the system
$2.50 for students and $3 for general admission. If 174 people attended the last gam
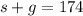
and the box collected $474
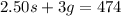
where s is the number of students and g the number of general admission
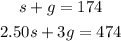
to solve the system
we solve a unknow and replace on the other equation ,for example I will solve s from the first equation
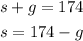
now I will replace the value of s on second equation
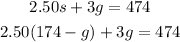
simplify

and solve for s
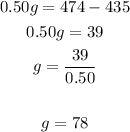
the value of g (number of general admission) is 78, From this one we can replace the value of g on any equation to solve s
I will replace on the furst equation solved to s
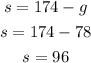
then the value of s (number of students ) is 96
The box officed sold 78 general admission ticjets and 96 students tickets