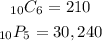Question

O PROBABILITY AND STATISTICSComputing permutations and combinationsEvaluate 10C6 and 10510% = 0P₁ = 010 5I need help with this math problem.

Answer 1

Step-by-step explanation

First part

The formula for combinations is:

`_nC_r=(n!)/((n-r)!r!)`

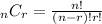
On the other hand, n! is the product of all positive integers less than or equal to n. For example:

`3!=3*2*1=6`

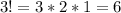
Then, we have:

`\begin{gathered} _nC_r=(n!)/((n-r)!r!) \\ _(10)C_6=(10!)/((10-6)!6!) \\ _(10)C_6=(10!)/(4!6!) \\ _(10)C_6=(10*9*8*7*6*5*4*3*2*1)/((4*3*2*1)(6*5*4*3*2*1)) \\ _(10)C_6=(3,628,800)/(24*720) \\ _(10)C_6=(3,628,800)/(17,280) \\ _(10)C_6=210 \end{gathered}`

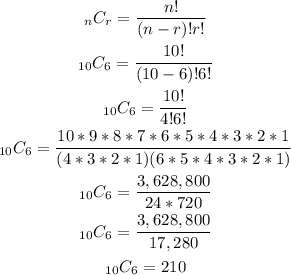
Second part

The formula for permutations is:

`_nP_r=(n!)/((n-r)!)`

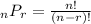
Then, we have:

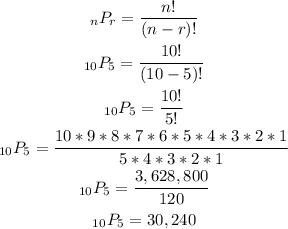
`\begin{gathered} _(n)P_(r)=(n!)/((n-r)!) \\ _(10)P_5=(10!)/((10-5)!) \\ _(10)P_5=(10!)/(5!) \\ _(10)P_5=(10*9*8*7*6*5*4*3*2*1)/(5*4*3*2*1) \\ _(10)P_5=(3,628,800)/(120) \\ _(10)P_5=30,240 \end{gathered}`Answer
`\begin{gathered} _(10)C_(6)=210 \\ _(10)P_(5)=30,240 \end{gathered}`