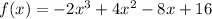We need to find a polynomial function f(x) with degree 3 and zeros 2 and 2i, such that:
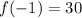
Since 2i is a zero, -2i is also a zero of this function. Thus, we have:
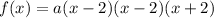
where a is a constant.
Expanding the expression on the right side, we obtain:
![\begin{gathered} \\ f(x)=a(x-2)\lbrack x²-(2i)²\rbrack \\ \\ f(x)=a(x-2)(x²-4i²),\text{ i^^b2=-1} \\ \\ f(x)=a(x-2)(x²+4) \\ \\ f(x)=a(x³-2x²+4x-8) \end{gathered}]()
Now, using f(-1) = 30, we obtain:
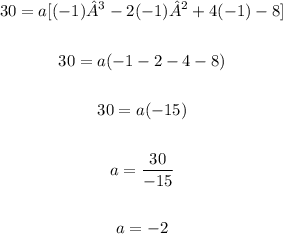
Therefore, the function is:
Answer