We have to find the angle at vertex J.
We know the shortest arc JK and the shortest arc JL.
As a property of the arcs, the inscribed angle
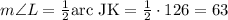 We can apply the same property to angle K:
We can apply the same property to angle K:
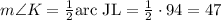
Now we have two angles of the triangle. We know that the sum of the measures of the interior angles of a triangle is equal to 180°, so we can write:
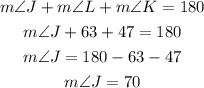
Answer: The angle at vertex J is 70 degrees.
NOTE: we could have solve it applying the relation between inscribed angles and arcs with angle J as:
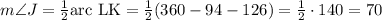
The arc LK is the full circle, 360°, less the other arcs, 94° and 126°.