Question

Determine the quadrant in which the terminal side of θ lies, subject to both given conditions.csc θ < 0, tan θ< 0

Answer 1

Case: Quadrants of trigonometry

Given:

csc θ < 0, tan θ< 0

Required: To find the quadrant the value falls into

Method:

Step 1: First we identify the four(4) major quadrant

Here,

I quadrant. All trigonometry functions are positive

II quadrant. Only sine is positive

III quadrant. Only tangent is positive

IV quadrant. Only Cosine is positive

Step 2:

`csc\theta=\frac{\text{ 1}}{sin\theta}<0`

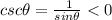
Only the III and IV are negative here.

Step 3: We try the second condition

`tan\theta<0`

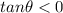
Here only the IV out of the (III) and (IV) will be negative

Final answer:

Only Quadrant (IV) satisfies the condition. Option (D)