Question

2. Write an equation of the ellipse with foci at (0, +2) and co-vertices at （+1, 0）.དུ དུའི - 1།14︽ 》སོ – །

Answer 1

Given,

The foci of the ellipse is (0, +2)(0.-2)

The co vertices of the ellipse is (1, 0)(-1, 0)

The genral equation of ellipse is,

`(x^2)/(a^2)+(y^2)/(b^2)=1`

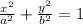
The equation of the foci is,

`\begin{gathered} (0,\text{ }\pm c)=(0,\text{ }\pm2) \\ \text{The value of c is 2.} \end{gathered}`

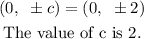
The equation of co vertices is,

`\begin{gathered} (\pm a,\text{ 0)=(}\pm1,\text{ 0)} \\ \text{The value of a is 1.} \end{gathered}`

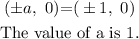
we know that,

`\begin{gathered} b^2=a^2+c^2 \\ b=\sqrt[]{5} \end{gathered}`

Substituting the value then,

`\begin{gathered} (x^2)/(1^2)+\frac{y^2}{\sqrt[]{5}^2}=1 \\ x^2+(y^2)/(5)=1 \end{gathered}`

Hence, option d is correct.